36  FAQ

36.1 用 R 画地图

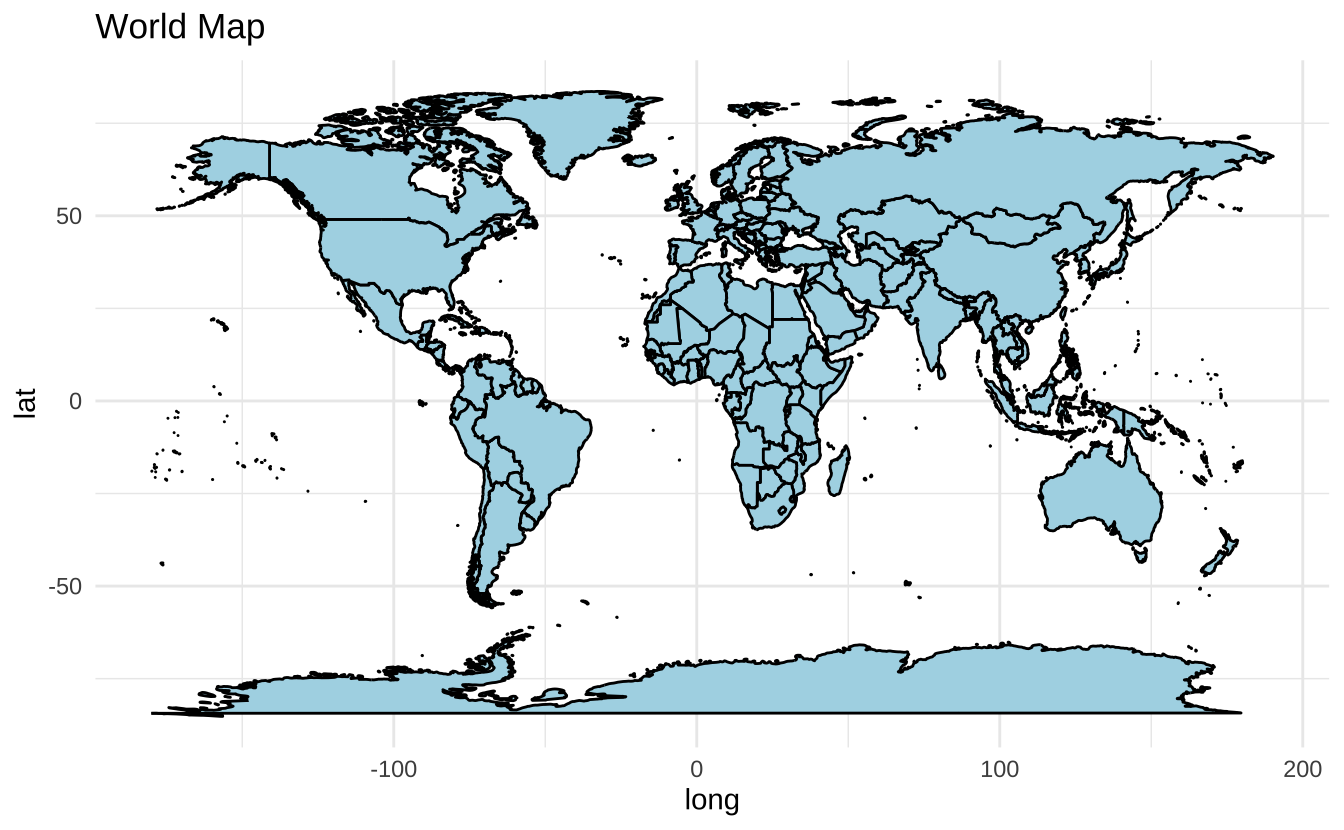
下面是一个使用 ggplot2 绘制世界地图的 R 代码示例。

library(ggplot2)
library(maps)

# 获取世界地图数据
world_map = map_data("world")

# 绘制地图
p = ggplot(world_map, aes(x = long, y = lat, group = group)) +
  geom_polygon(fill = "lightblue", color = "black") +
  theme_minimal() +
  labs(title = "World Map")

# 显示地图
print(p)

如果需要绘制特定国家或区域的地图，例如中国，可以这样做：

china_map = map_data("world", region = "Russia")

p_china = ggplot(china_map, aes(x = long, y = lat, group = group)) +
  geom_polygon(fill = "lightblue", color = "black") +
  theme_minimal() +
  labs(title = "Russia Map")

print(p_china)

这个示例使用 maps 包的 map_data("world") 获取世界地图数据，并用 ggplot2 绘制。你可以更改 fill 和 color 参数来自定义颜色。

36.2 找不到包，找不到函数，找不到文件

这是每个人都常常会掉进去的坑。

找不到包怎么样？

在 R 语言中，如果使用 library("package") 后提示找不到包，那么说明该包没有安装成功。请参照 Section 4.3.1 部分安装缺失的包。

找不到函数怎么办？

如下面的错误提示：Error in read_csv("file") : could not find function "read_csv"，说明函数对应的包还没有载入。使用 library("readr") 包载入即可使用。不同的函数来自于不同的包，如果不知道函数所在的包可以在 R 终端输入 ??read_csv 查找函数所属的包（可能会有多个包提供相同名字的函数）。

找不到文件怎么办？

找不到文件通常是路径写得不对。在访问文件时，可以使用相对路径或绝对路径两种方式：

  • 相对路径是基于当前工作目录 (getwd()) 的路径。例如，如果你的文件 data.xlsx 在当前目录下，则可以用 "data.xlsx" 访问它；如果在 data 目录下，则使用 "data/data.xlsx"。相对路径更灵活，适用于在不同环境运行相同代码时无需修改路径。

  • 绝对路径是文件在系统中的完整路径，例如 "/Users/username/project/data.xlsx"（macOS/Linux）或 "C:/Users/username/project/data.xlsx"（Windows）。它不会受当前工作目录影响，但在不同设备或用户环境下必然需要调整。

在 R 中：

  • list.files()、file.exists() 和 read_excel() 等函数支持相对路径和绝对路径。
  • 使用 normalizePath("path") 可将相对路径转换为绝对路径，避免路径混乱。
  • setwd("path") 可更改当前工作目录，但通常不推荐在脚本中使用，以免影响其他代码的执行环境。

36.2.1 中文用户名导致的路径问题

有不少同学在系统中使用了中文的用户名，这会导致路径问题。需要通过修改用户名的办法才能根本解决。

在 Windows 系统中，可以通过以下步骤修改用户名：

  • 在“设置”中找到“账户”。
  • 新建一个本地账户，将其设置为管理员权限。
  • 退出当前账户，登录新建的账户。
  • 在新建的账户下面操作。
  • 旧账户可以先保留，等待半年后或者磁盘空间紧张时，删除原来的账户。

36.3 批量线性回归总表

来自同学汪意茹的提问：有多个变量和自变量，想分别计算两两之间的线性回归模型，将参数以表格输出。

可以使用 lm() 进行线性回归，并提取所需的统计量，最终整理成一个表格。下面是 R 代码：

# 示例数据
set.seed(123)
n = 100
Y = as.data.frame(matrix(rnorm(n * 5), ncol = 5))
X = as.data.frame(matrix(rnorm(n * 5), ncol = 5))
colnames(Y) = paste0("Y", 1:5)
colnames(X) = paste0("X", 1:5)

# 计算线性回归结果
results = data.frame()
for (y in colnames(Y)) {
  for (x in colnames(X)) {
    model = lm(Y[[y]] ~ X[[x]])
    summary_model = summary(model)
    
    # 提取统计量
    slope = coef(model)[2]
    intercept = coef(model)[1]
    f_stat = summary_model$fstatistic[1]
    df1 = summary_model$fstatistic[2]
    df2 = summary_model$fstatistic[3]
    p_value = pf(f_stat, df1, df2, lower.tail = FALSE)
    r_squared = summary_model$r.squared
    
    # 存入结果
    results = rbind(results, data.frame(
      Dependent = y, Independent = x,
      Slope = slope, Intercept = intercept,
      F = f_stat, df1 = df1, df2 = df2,
      p_value = p_value, R_squared = r_squared
    ))
  }
}

# 查看结果
kableExtra::kable(results)
Dependent Independent Slope Intercept F df1 df2 p_value R_squared
X[[x]] Y1 X1 -0.0549252 0.0880826 0.3136684 1 98 0.5767158 0.0031905
X[[x]]1 Y1 X2 -0.0305091 0.0858404 0.1158822 1 98 0.7342728 0.0011811
X[[x]]2 Y1 X3 0.1641000 0.0730321 3.3410885 1 98 0.0706125 0.0329687
X[[x]]3 Y1 X4 -0.0196157 0.0922417 0.0500912 1 98 0.8233706 0.0005109
X[[x]]4 Y1 X5 0.0098457 0.0905949 0.0118710 1 98 0.9134615 0.0001211
X[[x]]5 Y2 X1 0.1179343 -0.1025582 1.3015941 1 98 0.2567026 0.0131075
X[[x]]6 Y2 X2 0.0734598 -0.0965540 0.6016299 1 98 0.4398246 0.0061016
X[[x]]7 Y2 X3 -0.0317125 -0.1041893 0.1076404 1 98 0.7435466 0.0010972
X[[x]]8 Y2 X4 -0.0416729 -0.1036466 0.2017709 1 98 0.6542870 0.0020547
X[[x]]9 Y2 X5 -0.0867070 -0.1092109 0.8272319 1 98 0.3653057 0.0083705
X[[x]]10 Y3 X1 0.0184264 0.1212445 0.0325083 1 98 0.8572890 0.0003316
X[[x]]11 Y3 X2 0.0080233 0.1216658 0.0073929 1 98 0.9316561 0.0000754
X[[x]]12 Y3 X3 -0.1081812 0.1319186 1.3141021 1 98 0.2544446 0.0132318
X[[x]]13 Y3 X4 -0.0481185 0.1249685 0.2790104 1 98 0.5985447 0.0028390
X[[x]]14 Y3 X5 -0.0134448 0.1202071 0.0204444 1 98 0.8865965 0.0002086
X[[x]]15 Y4 X1 -0.0994960 -0.0404316 0.7987189 1 98 0.3736662 0.0080843
X[[x]]16 Y4 X2 -0.0644415 -0.0458662 0.4003737 1 98 0.5283700 0.0040688
X[[x]]17 Y4 X3 0.1726759 -0.0545047 2.8425657 1 98 0.0949789 0.0281882
X[[x]]18 Y4 X4 -0.1630233 -0.0209656 2.7450284 1 98 0.1007557 0.0272473
X[[x]]19 Y4 X5 0.2496455 -0.0314315 6.2696003 1 98 0.0139343 0.0601287
X[[x]]20 Y5 X1 0.2177588 0.1150621 4.3702769 1 98 0.0391590 0.0426909
X[[x]]21 Y5 X2 -0.0062566 0.1049147 0.0041439 1 98 0.9488044 0.0000423
X[[x]]22 Y5 X3 -0.1377758 0.1204377 1.9779037 1 98 0.1627745 0.0197834
X[[x]]23 Y5 X4 -0.0372328 0.1093355 0.1537924 1 98 0.6957888 0.0015669
X[[x]]24 Y5 X5 -0.0155561 0.1055524 0.0252305 1 98 0.8741209 0.0002574

这个代码的核心逻辑：

  • 生成 5 个因变量和 5 个自变量的随机数据。
  • 使用 lm() 进行回归，并提取斜率、截距、F 统计量、自由度（df1, df2）、p 值和 R²。
  • 结果整理成 data.frame 并输出。

你可以用自己的数据替换 Y 和 X，代码仍然适用。

Tip

自由度是什么?

即如何理解类似下面的结果。

Call:
lm(formula = y ~ x, data = data.frame(x = 1:10, y = 21:30))

Residuals:
       Min         1Q     Median         3Q        Max 
-4.751e-15 -2.337e-15 -5.166e-16  9.302e-16  9.668e-15 

Coefficients:
             Estimate Std. Error   t value Pr(>|t|)    
(Intercept) 2.000e+01  2.891e-15 6.919e+15   <2e-16 ***
x           1.000e+00  4.659e-16 2.147e+15   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.231e-15 on 8 degrees of freedom
Multiple R-squared:      1, Adjusted R-squared:      1 
F-statistic: 4.608e+30 on 1 and 8 DF,  p-value: < 2.2e-16

自由度（Degrees of Freedom, DF）在回归分析中表示用于估计统计参数的独立数据点的数量。不同的自由度在回归分析中有不同的含义：

  1. 回归自由度（df1）：回归模型的自由度，等于自变量的个数（不包括截距）。在简单线性回归中，只有一个自变量，所以 df1 = 1。

  2. 残差自由度（df2）：误差项的自由度，计算公式是 n - k - 1，其中：

    • n 是样本大小，
    • k 是自变量的个数（不包括截距），
    • 1 是因为估计了截距。

在你的回归结果中：

  • F-statistic: 4.608e+30 on 1 and 8 DF，表示：
    • df1 = 1（因为只有一个自变量 x）。
    • df2 = 8（样本量 n = 10，减去 1 个自变量和 1 个截距，即 10 - 1 - 1 = 8）。

总结：

  • 回归自由度（df1）= 1（自变量 x）。
  • 残差自由度（df2）= 8（数据点 10 个，去掉 1 个自变量和 1 个截距）。

36.4 多变量分布和相关性作图

来自同学汪意茹的提问：如何绘制多变量之间的关系图？

使用 GGally 包中的 ggpairs 函数可以绘制多变量之间的关系图。

下面是一个可复现的示例：

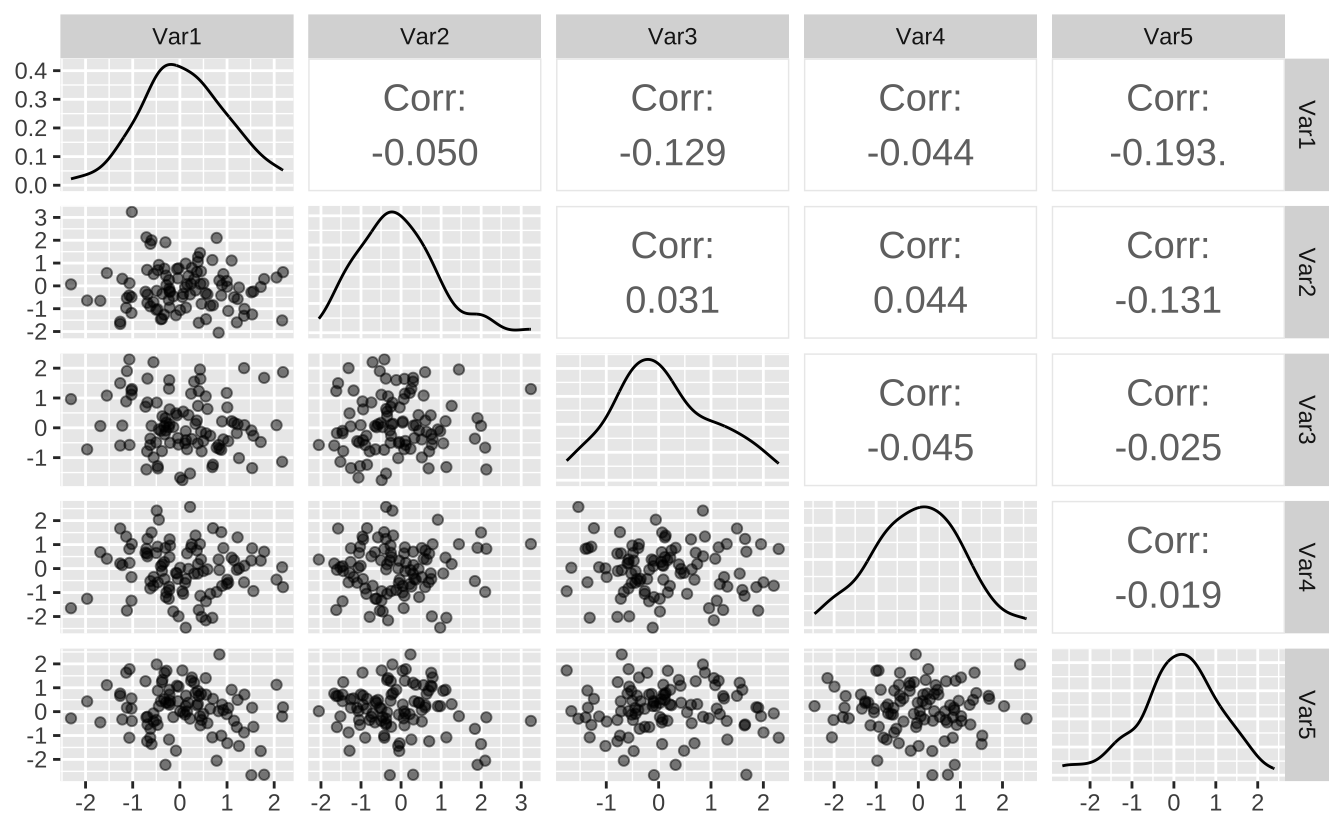
library(GGally)
library(ggplot2)

# 生成示例数据
set.seed(123)
df = as.data.frame(matrix(rnorm(100 * 5), ncol = 5))
colnames(df) = paste0("Var", 1:5)

# 绘制变量间的关系
ggpairs(df, 
        lower = list(continuous = wrap("points", alpha = 0.5)),  # 下三角：散点图
        diag = list(continuous = wrap("densityDiag")),          # 对角线：密度图
        upper = list(continuous = wrap("cor", size = 5)))       # 上三角：相关系数

上面的代码中，首先生成了一个 100 行 5 列的数据框，然后使用 ggpairs 函数绘制了变量间的关系图。其中，

  • lower 参数用于指定下三角的图形，这里使用了 points 函数绘制散点图，alpha 参数用于指定透明度；
  • diag 参数用于指定对角线的图形，这里使用了 densityDiag 函数绘制密度图；
  • upper 参数用于指定上三角的图形，这里使用了 cor 函数绘制相关系数图，size 参数用于指定相关系数的字体大小。

GGally 包还提供了其他的图形函数，例如 barDiag、boxplotDiag、dotplotDiag、histDiag、qqDiag、rcorr、rcorrDiag、rcorrPlot、rcorrPlotDiag、smoothDiag、textDiag 等，可以根据需要选择合适的图形函数。